Maximizing inner product in the intersection of two hyperspheres (2つの超球の共通部分内で内積を最大化する)
Problem setup (問題設定)
Given vectors \(a, b, h\in \mathbb{R}^n\) and positive numbers \(p, q > 0\), we would like to maximize the inner product \(h^\top z\) on condition that \(z\) is in the intersection of two hyperspheres \(S_1 = \{ z \mid \|z - a\| \leq p \}\) and \(S_2 = \{ z \mid \|z - b\| \leq q \}\).
What we would like to compute are summarized as \(f\) and \(z^*\) below:
\(f = \max_{ z\in S_1 \cap S_2 } h^\top z,\)
\(z^* = \mathrm{arg}\max_{z\in S_1 \cap S_2} h^\top z.\)
(i.e., \(h^\top z^* = f\).)
Intuitively, since we consider the inner product, what we would like to find is the largest vector among \(S_1 \cap S_2\) having the largest magnitude for the direction of \(h\) (see the figure below).
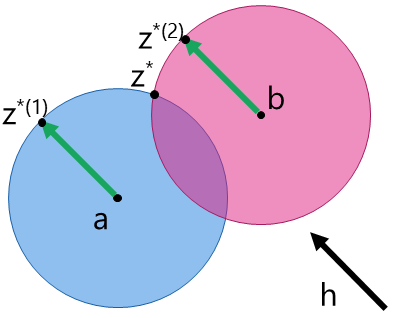
ベクトル \(a, b, h\in \mathbb{R}^n\) および正の実数 \(p, q > 0\) について、 ベクトル \(z\) は二つの超球 \(S_1 = \{ z \mid \|z - a\| \leq p \}\) および \(S_2 = \{ z \mid \|z - b\| \leq q \}\) の積集合の中にあるとする。 このとき、内積 \(h^\top z\) を最大化するような \(z\) は何であるだろうか。
これは、以下の \(f\) および \(z^*\) を得ることともいえる:
\(f = \max_{ z\in S_1 \cap S_2 } h^\top z,\)
\(z^* = \mathrm{arg}\max_{z\in S_1 \cap S_2} h^\top z.\)
(つまり、\(h^\top z^* = f\).)
直感的には、求めたいのが内積であるのだから、\(S_1 \cap S_2\) 内のベクトルで、\(h\) の向きに大きさが最も大きいものを求めればよい(上図参照)。
Solution (答え)
Step 1: Judge whether the optimum in question (optimum for two hyperspheres) is calculated as the optimum of either hypersphere (求めたいものは2つの超球についての最適値だが、それを1つの超球の最適値として得られるか判定する)
First we define the followings:
\(f_1 = \max_{z\in S_1} h^\top z,\)
\(f_2 = \max_{z\in S_2} h^\top z,\)
\(z^*_1 = \mathrm{arg}\max_{z\in S_1} h^\top z,\)
\(z^*_2 = \mathrm{arg}\max_{z\in S_2} h^\top z.\)
Then \(z^*_1\) and \(z^*_2\) are computed as:
\(z^*_1 = a + \frac{p}{\|h\|}h,\)
\(z^*_2 = b + \frac{q}{\|h\|}h.\)
Therefore,
- If \(z^*_1\in S_2\), then \(z^* = z^*_1\) and thus \(f = f_1 = h^\top z^*_1\).
- If \(z^*_2\in S_1\), then \(z^* = z^*_2\) and thus \(f = f_2 = h^\top z^*_2\).
- Otherwise, go to step 2.
Step 2: Calculate the optimum specifically when the optimum is not obtained as the optimum of either hypersphere (最適値が1つの超球の最適値として得られない場合に、具体的に計算する)
In this case, \(z^*\) is calculated as
\[z^* = c + \frac{\zeta}{\|\mu\|}\mu,\]where
\(d = \|b - a\|,\)
\(\omega = \frac{1}{2} - \frac{q^2 - p^2}{2 d^2},\)
\(c = a + \omega(b - a),\)
\(\zeta^2 = p^2 - \omega^2 d^2,\)
\(L = \frac{h^\top(b - a)}{d^2},\)
\(\mu = h - L(b - a).\)
Note for Step 1
The condition \(z^*_1\in S_2\) (the similar for \(z^*_2\in S_1\)) clearly holds if \(S_1 \subseteq S_2\). However, even if \(S_1 \subseteq S_2\) does not hold, \(z^*_1\in S_2\) may hold.
We present the following figures again in order to explain these cases above. Figure 1 is the case of \(z^*_1\in S_2\) and therefore \(f = f_1\) (\(z^* = z^*_1\)). Figure 2 is the case of neither \(z^*_1\in S_2\) nor \(z^*_2\in S_1\). As seen in the figure, in the second case the optimum \(z^*\) is found on the intersection of two hyperspheres. This is proved in the next step.
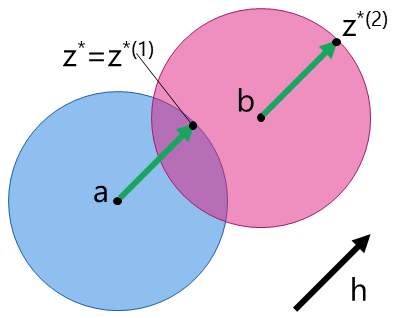
Figure 1: An example of being \(z^*_1\in S_2\) and therefore \(f = f_1\) (\(z^* = z^*_1\)).

Figure 2: An example of being neither \(z^*_1\in S_2\) nor \(z^*_2\in S_1\).
Proof of Step 2
If neither \(f = f_1\) nor \(f = f_2\) (i.e., \(z^*_1\in S_2\) nor \(z^*_2\in S_1\)), how \(z^*\) should be?
Since \(S_1 \cap S_2\) is a closed finite convex set, \(z^*\) must reside on the surface of \(S_1 \cap S_2\). Here, the surface of \(S_1 \cap S_2\) can be divided into three components:
- Component 1: surface of \(S_1\) but not of \(S_2\) (i.e., surface of \(S_1\) and also interior of \(S_2\)),
- Component 2: surface of \(S_2\) but not of \(S_1\) (i.e., surface of \(S_2\) and also interior of \(S_1\)), or
- Component 3: surface of both \(S_1\) and \(S_2\) (i.e., the intersection of surfaces of \(S_1\) and \(S_2\)).
If \(z^*_1\) resides on the component 1, then \(z^* = z^*_1\) must hold since \(z^*_1\in S_2\). Similarly, if \(z^*_2\) resides on the component 2, then \(z^* = z^*_2\) must hold since \(z^*_2\in S_1\). So, what we should consider is the component 3: the intersection of surfaces of \(S_1\) and \(S_2\).
Let \(T\) be the intersection of surfaces of \(S_1\) and \(S_2\), that is,
\[T = \{ z \mid \|z - a\| = p, \|z - b\| = q \}.\]Then, let us calculate \(T\) more specifically. By Lemmas 1 through 3, we can prove that it is equivalent to
\(T = \{ z | \|z - c\| = \zeta, z^\top(b - a) = k\},\)
where
\(c = a + \omega(b - a),\)
\(\omega = \frac{1}{2} - \frac{q^2 - p^2}{2 d^2},\)
\(\zeta^2 = p^2 - \omega^2 d^2,\)
\(k = \frac{\|b\|^2 - \|a\|^2 - (q^2 - p^2)}{2}.\)
So, \(T\) is a surface of a hypersphere on the (n-1)-dimensional subspace \(z^\top(b - a) = k\).
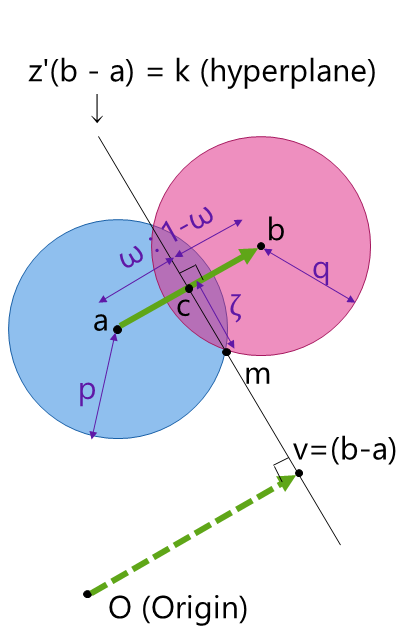
To maximize \(h^\top z\) on this \(T\), we need to take \(z\) for the same direction as \(h\) as possible: due to the constraint that \(z\) must be on \(T\), we may not take \(z = \frac{\zeta}{\|h\|} h\). To maximize this, we do the followings:
- Let us decompose \(h\) into the vector in the subspace (denoted by \(\mu\in \mathbb{R}^n\)) and perpendicular to the subspace (represented as \(L(b - a)\), where \(L\in \mathbb{R}\)), that is, \(\mu = h - L(b - a)\) subject to \(\mu^\top(b - a) = 0\).
- This is solved as \(L = \frac{h^\top(b - a)}{d^2}\).
- Take \(z = c + \frac{\zeta}{\|\mu\|} \mu\) to maximize \(h^\top z\).
Therefore, \(z^* = c + \frac{\zeta}{\|\mu\|} \mu\) if neither \(f = f_1\) nor \(f = f_2\).
Lemmas
Lemma 1
Let \(a\), \(b\) in \(\mathbb{R}^n\), and
\(T = \{ z \in \mathbb{R}^n \mid \|z - a\| = p, \|z - b\| = q \}.\)
Then, \(T\) is in certain hyperplane, that is, there exists \(v\in \mathbb{R}^n\) and \(k\in \mathbb{R}\) such that \(\forall m \in T \to m^\top v = k\).
Here, let \(H[T]\) be the hyperplane defined above.
Proof
Because \(\|m - a\| = p\) and \(\|m - b\| = q\), we have
\(\|m\|^2 - 2a^\top m + \|a\|^2 = p^2,\)
\(\|m\|^2 - 2b^\top m + \|b\|^2 = q^2.\)
Taking the difference of them, we have
\(2(a - b)^\top m + \|b\|^2 - \|a\|^2 = q^2 - p^2\)
and therefore
\(v = b - a,\)
\(k = \frac{\|b\|^2 - \|a\|^2 - (q^2 - p^2)}{2}.\)
Lemma 2
Let \(a\) and \(b\) be points in Lemma 1.
Let \(c = a + \omega(b - a)\) (\(0 \leq \omega \leq 1\)), that is, \(c\) is a point on the line segment between \(a\) and \(b\).
Then, \(c\) is on the hyperplane \(H[T]\) if
\(\omega = \frac{1}{2} - \frac{q^2 - p^2}{2 d^2}.\)
Proof
If \(c\) is on the hyperplane \(H[T]\), \(\omega\) can be computed as
\([a + \omega(b - a)]^\top(b - a) = k.\)
As a result, \(\omega d^2 = k - a^\top(b - a) = \frac{d^2 - (q^2 - p^2)}{2}.\)
Lemma 3
\(T\) can be represented as the intersection of \(H[T]\) and “the surface of a hypersphere with center \(c\)”.
More specifically, There exists a positive real number \(\zeta > 0\) such that
For any \(m\in \mathbb{R}^n,\) \(m\in T\) in Lemma 1 holds if and only if \(m\) is on the hyperplane \(H[T]\) and also on the surface of the hypersphere \(\|m - c\| = \zeta\).
Proof
By the Pythagorean theorem, we can calculate as \(\zeta^2 = p^2 - \omega^2 d^2\). This \(\zeta\) assures the sufficiency of the theorem.
Let us prove the necessity, that is, any \(m\in T\) is on both \(H[T]\) and \(\|m - c\| = \zeta\), where the former is already proved as Lemma 1.
Calculating \(\|m - c\|^2\) we have
\(\|m - c\|^2 = \|c\|^2 - 2m^\top c + \|m\|^2\)
\(= \|c\|^2 - 2m^\top(a + \omega(b - a)) + \|m\|^2\)
\(= \|c\|^2 - 2m^\top a + \|m\|^2 - 2\omega m^\top(b - a)\)
\(= \|c\|^2 + p^2 - \|a\|^2 - 2\omega m^\top(b - a)\)
(By the assumption \(\|m - a\| = p\))
\(= \|c\|^2 + p^2 - \|a\|^2 - 2\omega k\)
(By Lemma 1)
\(= \|a\|^2 + \omega^2\|b - a\|^2 + 2\omega a^\top(b - a) + p^2 - \|a\|^2 - 2\omega k\)
\(= \omega[k - a^\top(b - a)] + 2\omega a^\top(b - a) + p^2 - 2\omega k\)
\(= \omega[a^\top(b - a) - k] + p^2\)
\(= p^2 - \omega^2 d^2.\)
Therefore, \(\zeta^2 = p^2 - \omega^2 d^2\) is proved to be the necessary and sufficient condition for the proposition.